Loss Functions in Machine Learning and LTR
Previously, decision theory was disscussed and an important part of is to evaluate a decision rule for decision making. Since the risk is the average loss \(L(\theta,d)\), different loss functions were used in Machine Learning models. Mean squared error (MSE) was mentioned as the most famous meausre by using squared error loss proposed by Gauss. Regression, Linear discriminant analysis (LDA) use squared error loss. The squared loss function tends to penalize outliers excessively, leading to slower convergence rates. There are other popular loss functions and they are applied in various Machine Learning and Deep Learning models. The plot shows the loss function for two class classification.
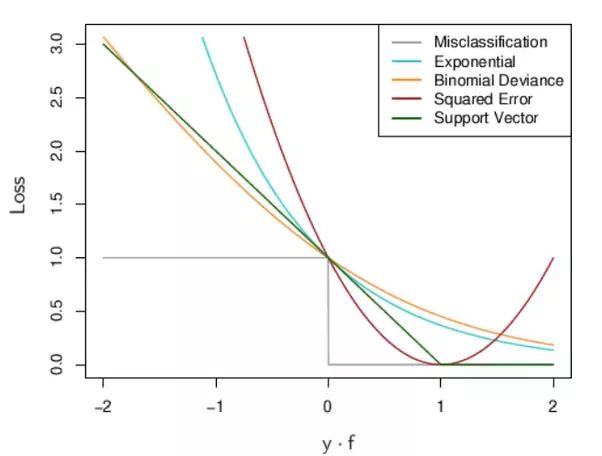
Loss Functions: “Loss vs y*f(x); \(y= \pm 1\), the prediction is f, with class prediction sign(f)”
1. Hinge loss
The hinge loss is a loss function used for “maximum-margin” classification, most notably for support vector machine (SVM).It’s equivalent to minimize the loss function \(L(y,f) = [1-yf]_+\).
With \(f(x) = h(x)^T \beta + \beta_0\), the optimization problem is loss + penalty: \[ \min_{\beta_0,\beta} \sum_{n=1}^{\infty}[1-y_if(x_i)]_+ + \frac{\lambda}{2}||\beta||^2 \]
2. Exponential loss
The exponential loss is convex and grows exponentially for negative values which makes it more sensitive to outliers. The exponential loss is used in the AdaBoost algorithm. The principal attraction of exponential loss in the context of additive modeling is computational. The additive expansion produced by AdaBoost is estimating onehalf of the log-odds of P(Y = 1|x). This justifies using its sign as the classification rule.
The population minimizer is: \[f^*(x) = \arg\min_{f(x)} E_{Y|x}(e^{-Yf(x)}) = \frac{1}{2} log\frac{Pr(Y = 1|x)}{Pr(Y = -1|x)}\] or \[Pr(Y = 1|x) = \frac{1}{1+e^{-2f*(x)}}\] 3. Logistic loss(Binomial Deviance)
The logistic loss is also called as binomial log-likelihood loss or cross entropy loss. It’s used for logistic regression and in the LogitBoost algorithm. The cross entropy loss is ubiquitous in deep neural networks/Deep Learning.
The binomial log-likelihood loss function is: \[l(Y,p(x)) = Y'logp(x) + (1-Y')log(1-p(x))\]
or the deviance \[-l(Y,f(x) = log(1+e^{-2Yf(x)})\]
Summary Table
| Loss Function | \(L[y,f(x)]\) | Minimizing Function | Advantage/Disadvantage |
|---|---|---|---|
| Squared loss | \([y-f(x)] = [1-yf(x)]^2\) | \(2Pr(Y=+1|x)-1\) | easy cross validation of regularization parameters/slower convergence rates |
| Hinge loss | \([1-yf]_+\) | \(sign[Pr(Y=+1|x)-\frac{1}{2}]\) | support points/not differentiable at\(yf(x)=1\) |
| Exponential loss | \(\frac {1}{2} log(1+e^{-Yf(x)})\) | \(\frac{1}{2}log\frac{Pr(Y =+1|x)}{Pr(Y =-1|x)}\) | grows exponentially for negative values,more sensitive to outliers |
| Logistic loss | \(log(1+e^{-Yf(x)})\) | \(log\frac{Pr(Y =+1|x)}{Pr(Y =-1|x)}\) | grows linearly for negative values,less sensitive to outliers |
Similarities between loss functions:
Hinge loss, Exponential loss, Logistic loss have very similar tails, giving zero penalty to points well inside their margin and linear or exponential penalty to points on the wrong side adn far away. Squared error loss gives a quadratic penalty and points inside their own margin have a strong influence on othe model as well.
Exponential loss and Logistic loss have the same asymptotes as the SVM hinge loss but are rounded in the interrior.
The above popular loss functions are also used in deep learning, for example, Learing To Rank (LTR) for a Recommender System (RS). Differently from traditional machine learning problem that’s to predict the target either classification or regression, LTR optimizes the ranking accruacy instead of the prediction probability accuracy.
Ranking is useful in our daily life for Recommendation system like Netflix, Amazon; Information Retrieval like goole; Drug discovery; Bioinformatics. Generally speaking, there are three types of rankings: bipartie ranking, k-partite ranking, real-valued labels based ranking. RankSVM, RankBoost, RankNet with corresponding loss functions are used for the ranking problems. A seperate post will be written to further demonstrate LTR framework and how the loss functions are used.
Reference:
Hastie, T., Tibshirani, R., & Friedman, J. H. (2009). The elements of statistical learning: data mining, inference, and prediction. 2nd ed. New York: Springer. Computer Science & Artificial Intelligence Laboratory, MIT